Solving X = 2023: A Step-by-Step Guide & More!
Can a seemingly simple equation reveal a universe of mathematical concepts and real-world applications? The answer lies in the exploration of cubic equations, specifically those like x3 = 2023, a journey that unveils the elegance and power of mathematical principles.
The expression x x x, also represented as x3, forms the heart of this mathematical inquiry. This denotes a cubic equation, characterized by a variable, in this case 'x', raised to the power of three. The core objective here is to determine the value of 'x' that, when cubed, yields a result of 2023. In the realm of real numbers, every value of 'x' when cubed, will produce an output. This exploration goes beyond simple arithmetic; it dives into the foundational concepts of algebra, number theory, and even touches upon applications in various fields.
The equation x3 = 2023 poses a fundamental question: what number, when multiplied by itself three times, equals 2023? This is more than just a numerical exercise; it embodies the essence of cubic equations. The mathematical notation x3 encapsulates the operation of raising a number to the power of three, signifying x x x. This cubic equation is a mathematical puzzle prompting us to seek the value of x, ensuring that its cube matches 2023. To solve this, the cube root method is employed. To isolate 'x', we apply the cube root to both sides of the equation, effectively reversing the cubing operation.
Understanding the equation x3=2023 requires delving into a world where equations like this involve various mathematical concepts and techniques. In this pursuit, we encounter solution strategies and theorems, such as the rational root theorem, designed to unravel the mysteries of these equations. If we multiply x by itself three times, as in x x x, the result equates to x3. The equation x x x = 2023 implies finding an 'x' value where its product with itself thrice equals 2023. This forms the base of a cubic equation, which has profound implications.
The initial approximation is pivotal in finding an approximate solution to this equation. To unravel the unknown value of x, one might begin by making an initial guess or estimation. Through iterative methods and approximation techniques, we move closer to the precise solution. The journey of finding the cube root of 2023 is not just about arriving at a single numerical answer. It reveals the underlying principles of mathematical operations, allowing us to appreciate the beauty and intricacy of mathematical principles. Cubic equations have wide-ranging applications across diverse domains.
The equation x3=2023 can be written as (x3) = 2023. It is a mathematical problem encouraging us to find the value of 'x' so that when 'x' is cubed, the result is 2023. In this equation, solutions are rational integers with roots of p = 0 and not roots of q = 0. To solve it, we employ the Rational Root Theorem.
- Jameliz Benitez Smith What You Should Know Now Latest Info
- Searching Mandine More Discover Insights Info Now
Another intriguing facet involves an equation with the form | xx2023 = 2023. This illustrates an exciting area for mathematical investigation. As we delve into the intricacies of x3 = 2023, we acknowledge the significance of mathematics across various disciplines. Equations like these show how mathematical tools can unlock the complex relationships.
The world of mathematics is vast and varied, encompassing everything from basic arithmetic to complex calculations. The cubic equation x3 = 2023 presents an example of this range. To find the solution, we start by acknowledging that x x x is equivalent to x3. From there, we realize that understanding mathematical concepts such as the rational root theorem and the cube root method becomes essential. This means recognizing that the cube root method must be used to solve the problem. By applying this method, we aim to isolate 'x' and discover its specific value, which when cubed, results in 2023.
Beyond the purely mathematical, we see instances where the letter 'x' has other meanings. For example, there's the film series "xXx," an American spy fiction action franchise. Similarly, the use of 'x' appears when constructing Roman numerals. For example, two 'x's together signify 20 (XX = 20) in the Roman numeral system.
Roman numerals use seven symbols: I, V, X, L, C, D, and M. Each symbol holds a specific numerical value. We know that 'x' represents 10. Similarly, 'xx' represents 20. The Roman numeral 'xxxix' stands for 39. Understanding the concept of subtractive notation is vital here. For example, when dealing with 'xc', the value of 'x' is subtracted from the value of 'c'.
The mathematical equation x3 = 2023 may seem simple at first. Still, it represents more profound concepts such as cubic equations and the need to understand how to isolate 'x'. This requires using the cube root method. We can see that the fundamental structure of the equation involves a variable raised to the power of three.
The equation x3 = 2023 is essentially a mathematical riddle that asks us to identify an 'x' value where cubing it leads to 2023. To get to the solution, we may apply the cube root technique on both sides to eliminate the power. In other words, we separate 'x' by taking the cube root on both sides.
In mathematics, the equation x3 = 2023 has implications beyond simple calculations, as equations such as this will involve various concepts. In such problems, we may see solutions that are rational integers. These equations require the rational root theorem to be solved. If x is multiplied by itself three times, we get x3.
Let's delve into how one might approach this equation and discover the various related concepts and applications. The journey of finding the cube root of 2023 can become a learning opportunity, revealing the underlying principles.
Let us explore how to solve this equation and delve into the associated concepts and applications. To find the approximate solution we start with Initial approximation. This will lead us to the core of x3 = 2023 equation, which serves as the foundation of understanding mathematical ideas and how they are implemented in real life.
The problem asks us to solve the expression x x x = 2023. We can also write it as x3=2023, which is a cubic equation. To solve such equations, we employ several mathematical techniques. To solve the equation, we apply the cube root approach on both sides. This allows us to isolate 'x'. The cube root of 2023 then provides the solution.
The equation x x x = 2023 signifies that we need to find the product of x which, when multiplied three times, will equal 2023. This leads to a cubic equation, which can be represented as x3 = 2023. This highlights the need for an initial approximation to locate the solution. Such problems will often call for different equations and techniques.
This equation x3=2023 reminds us that the expression x x x can be written as x3, representing x raised to the power of 3. In mathematics, x3 is equivalent to multiplying x by itself three times. To find the value of 'x', we use the cube root method. The cube root is used to eliminate the power.
- Bolly4u Your Guide To Free Movies Entertainment Discover Now
- Doujindesu Down Quick Fixes Alternative Sites You Need
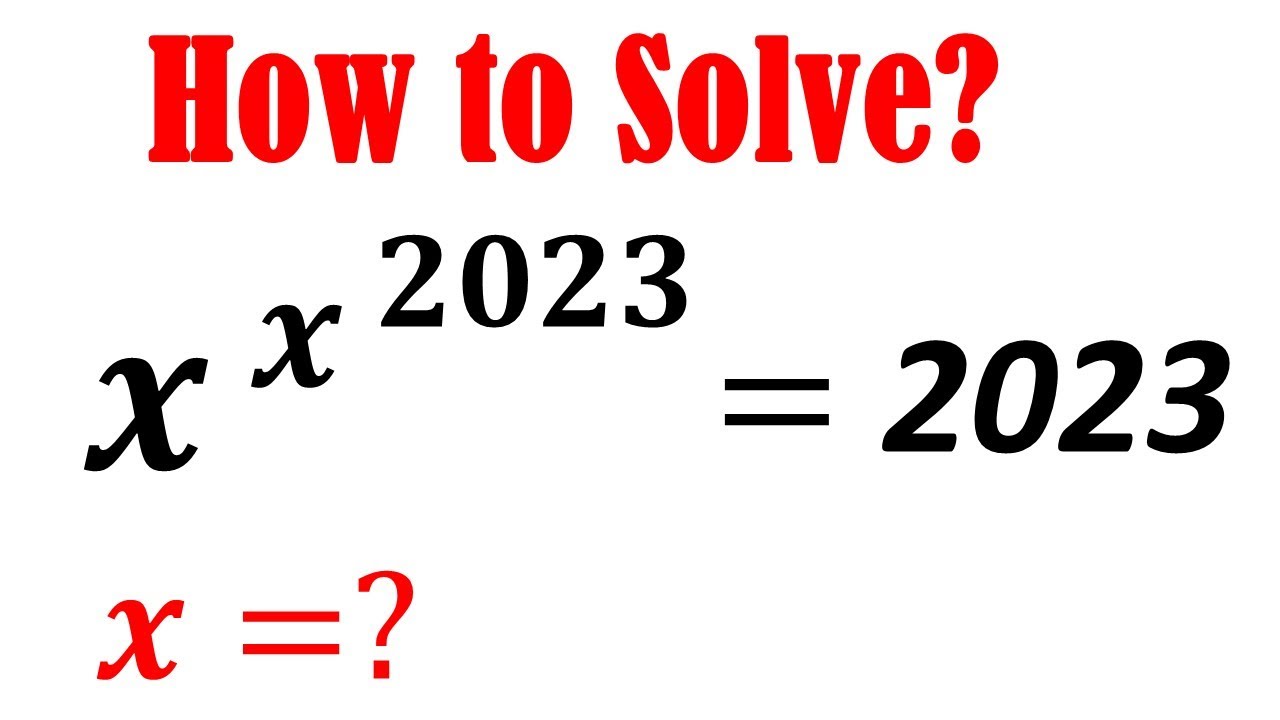
Math Olympiad Preparation x^x^2023=2023 A Nice Equation solving You
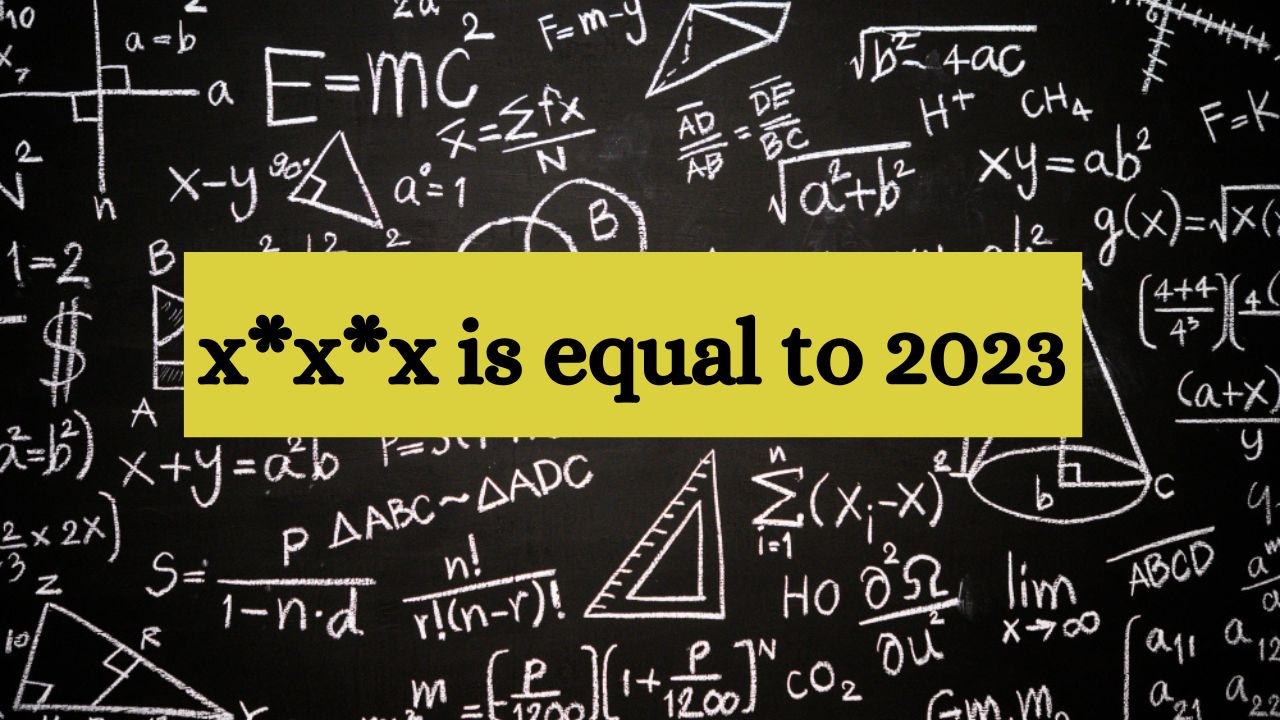
Solve the Equation “x*x*x is equal to 2023”

Unlocking the Mystery When Does xxx Equal 2023? by Muskan Medium