Unveiling X*X*X: Meaning, Solving & Applications In Math!
What profound insights can be unlocked by something as seemingly simple as "x x x"? This seemingly straightforward expression, far from being a mere string of symbols, is a gateway to understanding fundamental mathematical concepts and their surprising applications across diverse fields.
The expression "x x x" might appear basic, yet it encapsulates a fundamental mathematical operation: exponentiation. In mathematical terms, this is equivalent to x raised to the power of 3, often written as x or x3. This signifies that the variable 'x' is multiplied by itself three times. This concept is not merely an abstract mathematical construct; it is a crucial building block in algebra, calculus, and countless real-world applications.
The core of this concept, where x is multiplied by itself three times, is fundamental to understanding cubic equations and their applications. Consider the equation x = 8. This is a cubic equation, and solving it involves finding the value of 'x' that satisfies the equation. In this case, x = 2, because 2 2 2 = 8. This is a practical example illustrating the importance of grasping such concepts.
- Akshat Gupta Biography Books Achievements Your Complete Guide
- Exploring Tami Tsunami Leaks Onlyfans More Uncovered
Let's delve deeper. The expression x is a type of polynomial, specifically a cubic polynomial. Cubic polynomials, due to the presence of the exponent 3, are defined by their highest power being three. Such polynomials play a significant role in various mathematical models, from predicting the trajectory of a projectile to modeling economic growth.
One might encounter a slightly different, yet related, formulation: x + x + x + x = 4x. This equation, though elementary, unveils the core principles of algebra. Essentially, the left-hand side represents the repeated addition of 'x', which simplifies to 4 times 'x'. This is a foundational concept, providing a stepping stone to more intricate algebraic manipulations.
Further complexities emerge when we consider equations like x = 2. Here, the value of 'x' is not a whole number. Instead, 'x' is equal to the cube root of 2, denoted as 2, which is approximately 1.26. This example bridges the gap between real and imaginary numbers, highlighting the depth and multifaceted nature of mathematics.
- Viral Mms Scandals Latest News Updates On Leaks In 2024
- Hubflix Where To Watch Movies Online Features Risks Explored
The power of this concept extends to solving equations. Solving for 'x' in an equation like x = 2 involves isolating 'x' by taking the cube root of both sides of the equation. This process allows us to determine the value of the unknown variable.
In real-world applications, the concept of x and cubic equations is valuable. Imagine, for instance, modeling the volume of a cube, where each side is represented by 'x'. The volume (V) of the cube is calculated using the formula V = x. Understanding this simple relationship has wide-ranging implications in various fields, from architecture and engineering to physics and computer science.
Let's explore the practical side. Consider the task of calculating x = 2023. To solve this, we express the equation in its simplest form and then apply the cube root method. We take the cube root of both sides to isolate 'x'. This illustrates how seemingly complex problems can be solved by applying fundamental principles.
The flexibility of this mathematical concept also applies to finding solutions across multiple variables. The "solve for x" calculator and the concept itself enable one to find a solution to an equation or a system of equations. This capability is instrumental in solving real-world issues across many industries.
Mathematical equations and concepts serve as a foundation for understanding real-world phenomena. In the context of this, the simple idea of x multiplied by itself three times acts as a model, which allows one to evaluate and study a concept.
The ability to comprehend equations like x+x+x+x = 4x is crucial in understanding the principles that govern calculus and change. The systematic approach to the problem is part of understanding the equation.
Now we can explore more abstract applications. For example, the equation x + 2 = 0 represents an important moment in the study of maths in class 10. Understanding such equation is a starting point for understanding the principles which can be applied to real-life situations.
Mathematics, in its essence, is a symphony of interconnected ideas. Equations like x x x = x and x + x + x + x = 4x are not just abstract formulas; they are a testament to the human capacity for understanding and problem-solving. Each equation is a building block in a larger system, allowing us to model and understand the world around us. They serve as tools to unlock knowledge.
Here's a table summarizing the essence of x and related concepts:
| Concept | Description | Relevance |
|---|---|---|
| x x x | Represents x multiplied by itself three times. Equivalent to x. | Fundamental to understanding cubic equations, polynomials, and exponentiation. |
| x | X raised to the power of 3. | Core concept in algebra, calculus, and real-world applications. |
| Cubic Polynomials | Polynomials with the highest power of 3. | Used in various mathematical models, such as predicting trajectories. |
| x + x + x + x = 4x | Represents the repeated addition of x, simplified to 4x. | Foundation for understanding algebraic manipulations and calculus concepts. |
| Solving for x | Finding the value of x that satisfies an equation. | Applies to various disciplines, including engineering, science, and finance. |
| Cube Root | The inverse operation of cubing a number. | Used to solve cubic equations, such as x = 2. |
| Real-world Applications | Modeling volume, growth, and other phenomena. | Applications in architecture, engineering, physics, and computer science. |
In mathematics, it's also important to remember that various types of problems can be addressed. Equations and inequalities are not meant to be solved at a simple level, but to serve as a basis for solving more advanced math problems.
The process of solving for x, irrespective of the equation's complexity, consistently underscores the importance of using the correct approach to the problem. Understanding the relationships between variables, the operations at hand, and how they can be applied to determine a solution, is the key to unlocking the secrets hidden within each mathematical formulation.
The equation "x x x = 2" highlights the complexity of mathematics, crossing the boundaries between real and imaginary numbers. This crossover invites mathematicians to explore unknown domains and showcases the dynamic and multifaceted nature of mathematical ideas.
In a world driven by technology and data, mathematical principles are not merely a historical curiosity. The fundamental concepts, as presented here, are a powerful tool to tackle many problems. Through practice and conceptualization, one can harness the power of mathematics to unlock the hidden meanings of the world around us.
In essence, whether solving equations to a set of numbers, working out the sum of variables, or understanding the fundamental building blocks of mathematics, the equation x x x will continue to be a cornerstone. It is an important idea, allowing one to engage with the world on a deeper level and provides a unique framework for problem-solving.
We can see the depth of mathematics in the seemingly straightforward process of multiplying x by itself three times. It embodies the spirit of inquiry, the delight of discovery, and the power of human intellect to grasp, model, and manipulate the world.
- Odisha Viral Videos Social Media Safety Actresss New Series
- Michael Ches Wife Leslie Unveiling Their Relationship Secrets
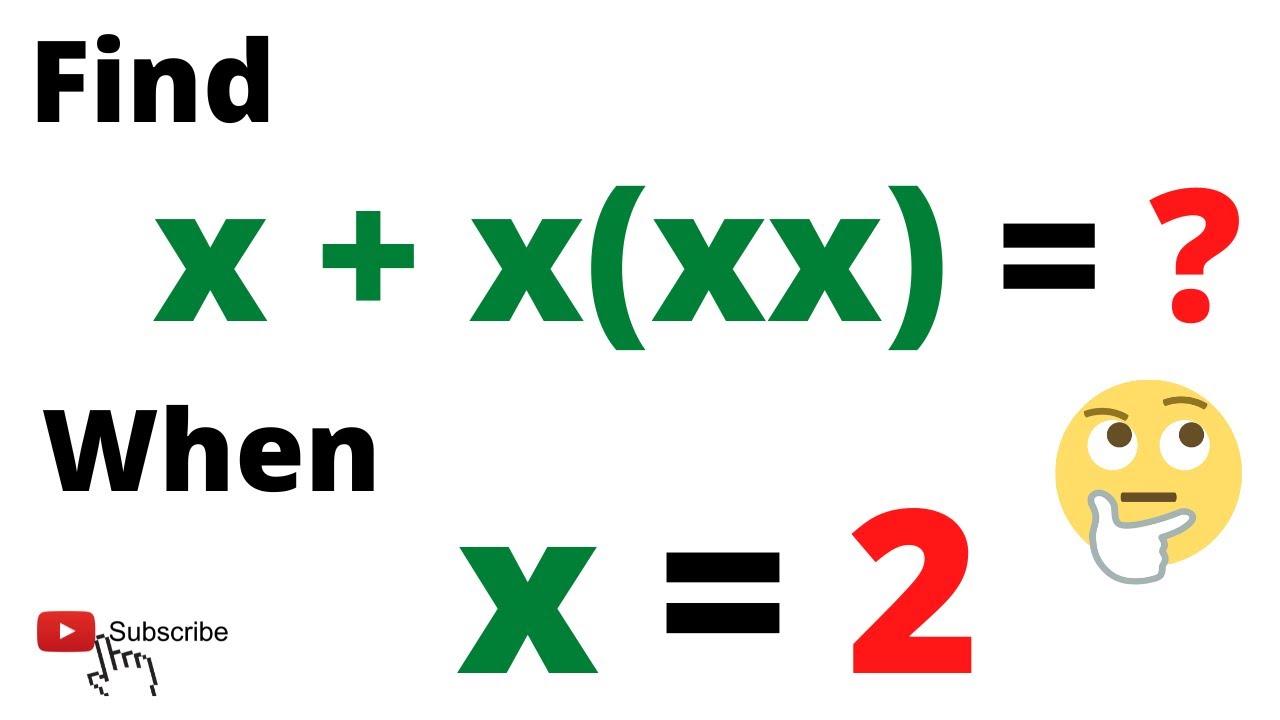
The value of x + x(xx) when x = 2 is Find the Answer in Seconds

Find X if X is Rational Number Such That X X X Equal to X

x*x*x is Equal to x*x*x equal to ? Knowledge Glow