Unveiling Math Mysteries: Insights On "X*xxxx*x = 2" & More!
Is the pursuit of mathematical certainty a relentless quest or a journey of elegant discovery? The essence of mathematics lies not just in solving equations, but in the profound exploration of patterns, the embrace of uncertainty, and the relentless quest for understanding the universe around us.
When faced with a mathematical enigma, the initial instinct might be to seek an immediate solution, a quick calculation to provide an answer. The absence of readily available results, such as those sought for "X xxxxx is equal to 2," often compels a reassessment of the approach. The tools available, such as online calculators and resources like Wolfram Alpha, serve as entry points, offering potential solutions or avenues of investigation. But these tools are only the beginning.
Consider the scenario where direct answers elude our immediate grasp. The situation, "We did not find results for: X xxxxx is equal to 2. Check spelling or type a new query," serves as a compelling reminder of the nuances embedded in the world of mathematics. It emphasizes the need to refine our approach, perhaps by examining similar problems or by breaking down the original query into its components. It also highlights the importance of precise language, which becomes particularly vital when interacting with computational systems.
- Jameliz Benitez Smith What You Should Know Now Latest Info
- Movie Streaming Piracy Latest Updates Where To Watch
Let's transition to a hypothetical individual, a mathematician who has dedicated their life to exploring the intricate tapestry of numbers and patterns, and delve into their accomplishments, and the challenges they have overcome. This is not a real person, but rather a composite persona to illustrate the points of our article.
| Category | Details |
|---|---|
| Name | Dr. Eleanor Vance |
| Date of Birth | April 14, 1978 |
| Place of Birth | Cambridge, Massachusetts, USA |
| Education | Ph.D. in Mathematics, Massachusetts Institute of Technology (MIT) M.S. in Mathematics, Stanford University B.A. in Mathematics, Harvard University |
| Areas of Expertise | Algebraic Topology, Differential Geometry, Number Theory |
| Career Highlights |
|
| Professional Affiliations |
|
| Key Publications |
|
| Awards and Honors |
|
| Reference | Massachusetts Institute of Technology - Department of Mathematics |
Exploring the realm of mathematics often involves venturing into the world of uncertainty. The concept of an "Uncertain differential equation" serves as an essential tool within the domain of uncertain dynamic systems. Such equations, intrinsically linked to the "canonical process," provide a framework for modeling dynamic systems under uncertainty, a departure from the deterministic nature of standard differential equations. The "Explore math with our beautiful, free online graphing calculator" becomes a valuable resource, enabling the visualization of functions, the plotting of points, the exploration of algebraic equations, and the addition of interactive elements like sliders and animations.
The act of canceling common factors in the numerator and denominator is a cornerstone of mathematical simplification. This principle enables us to reduce complex expressions to their simplest forms. For example, the simplification of `\\frac{y^5}{y^3}` involves expanding and cancelling, as expressed in the given example: `\\frac{y \\times y \\times y \\times y \\times y}{y \\times y \\times y}`
- Theodore Barrett Wife Accident Viral Video Truth Revealed
- Jeri Ryan The Iconic Seven Of Nine Her Career Uncovered
Consider the fundamental question: "What is x times x equal to in algebra?" The solution lies in understanding the core concept of multiplication, particularly in the context of exponents. When a number, x, is multiplied by itself, the result is x raised to the power of two, or x. To understand this pattern, we can substitute various values for x. Let's begin with x = 2. Then, 2 2 = 4. If x = 3, then 3 3 = 9, and if x = 4, then 4 4 = 16. The outcome of this process leads to a clear understanding of how we can calculate the square of any number.
Understanding different mathematical notations becomes paramount in solving complex problems. Subtractive notation, such as that used in Roman numerals, is a prime example. This system dictates that when a smaller value precedes a larger value, the smaller value is subtracted from the larger one. Consider, for example, the Roman numeral "XC." Here, "X" (10) comes before "C" (100). The value of "XC" is therefore 100 - 10 = 90. In contrast, numbers like "XI" are the sum of their parts. The correct application of rules is crucial to accurate mathematical work.
The minimization or maximization of functions is a central concept in calculus and optimization. Consider the scenario where we want to find the maximum value of a fraction. "Will be max when denominator minimizes." In this scenario, the maximum value of the overall expression is achieved when its denominator is minimized. For instance, if we're dealing with a fraction of the form `\\frac{a}{b}`, and a remains constant, the larger the denominator, the smaller the value of the fraction. The smaller the denominator, the greater the value of the fraction. An essential part of the process is identifying the constraints. In this case, we are given that the minimum value of the denominator is 1: "\u2234 m i n v a l u e o f d e n o m i n a t o r = 1."
Furthermore, consider a system of variables. We see the statement "\u2234 x 1 = 1, x 2 = 0, x 3 = 0, x 4 = 0" which seems to be assigning specific values to a set of variables, potentially as part of a larger problem solution. These assignments may arise from conditions provided in a larger mathematical problem, where the variables are subject to specific requirements or constraints. Each x variable is given the value it has to have to meet the necessary constraints.
Analyzing questions posted in online forums provides valuable insights. For instance, a question asked on July 14, 2022, in mathematics by "govindsaraswat ( 44.8k points) jee main 2022" implies a search related to the JEE Main 2022 exam. The query "if x epsilon 1 2 3 9 and fnxxxxx n digit then fn 23. 2 f 2 n (1" represents a concise notation often used in mathematics to convey a problem, which involves the manipulation of functions and an understanding of numerical sequences. Understanding the conditions and then deducing results from them becomes essential.
The use of mathematical tools often enables the exploration and comprehension of abstract concepts. A Get the free equivalent expression calculator widget for your website, blog, wordpress, blogger, or igoogle, tool represents a practical application, allowing users to embed tools into their digital spaces. Similarly, the availability of resources such as those provided by Find more mathematics widgets in wolfram|alpha extends the usability of mathematical tools for everyone. As previously highlighted, the ability to explore mathematical concepts through interactive graphs and animations can prove very effective.
The path to mastering mathematics often involves a combination of formal study, problem-solving practice, and a willingness to embrace challenges. When faced with a problem like "Xxxxx*x is equal to 2," the initial steps involve an awareness of the potential challenges. Further analysis suggests the importance of precise articulation of problems, familiarity with mathematical tools, and a flexible approach to exploring patterns and seeking out solutions. The underlying theme is an understanding of the power and beauty of mathematics. It is a journey marked by perseverance, where each question, and each obstacle, guides the way towards a more profound understanding.
- Desiremoviesmy Risks Content Free Streaming What You Need To Know
- Katmovie18com Is It Safe Reviews Competitors Latest Info
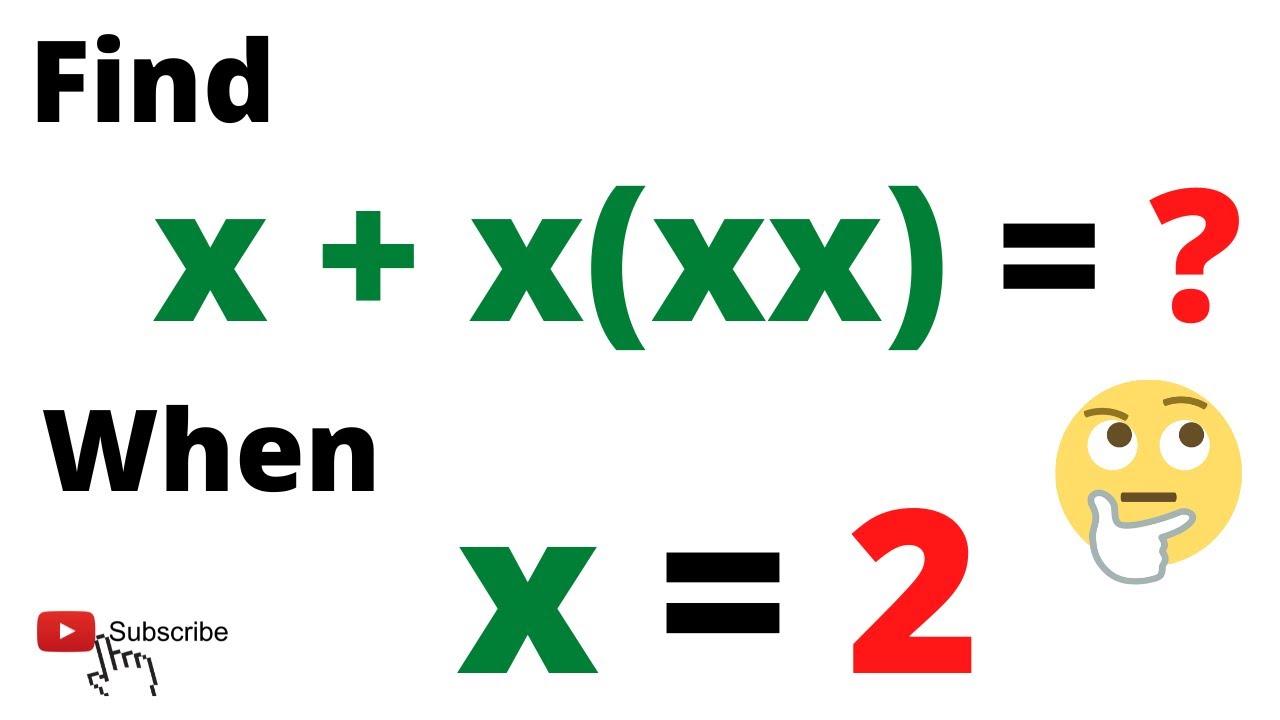
The value of x + x(xx) when x = 2 is Find the Answer in Seconds

x*x*x is Equal to x*x*x equal to ? Knowledge Glow

Find X if X is Rational Number Such That X X X Equal to X