Solving X = 2: Step-by-Step Guide & Solution
Can a single variable, when subjected to the seemingly simple operation of "cubing," unlock a precise numerical truth? The answer lies in the fascinating world of algebra, where equations like "xx x is equal to 2" offer a glimpse into the elegant dance between unknown quantities and fixed values.
The realm of mathematics is populated with enigmas that, when deciphered, illuminate the fundamental principles governing our universe. One such puzzle presents itself in the equation "x xx is equal to 2." This seemingly straightforward expression, however, conceals a journey of exploration, a voyage through the territories of variables, constants, and exponents, leading us to the precise value of 'x'.
At the heart of this mathematical exploration lies the variable 'x'. In the lexicon of algebra, 'x' serves as a placeholder, a versatile symbol that represents an unknown quantity. Our objective here is to find the value of 'x' that fulfills the condition dictated by the equation.
- Breaking Daisy Melanins Viral Video Biography What You Need To Know
- Nicole Wallace Gabriel Guevara What Really Happened
The equation "x xx is equal to 2" is, in essence, a compact representation of a fundamental mathematical principle. It implies that a certain number, when multiplied by itself three times, yields the result of 2. The expression 'x xx' can also be expressed in a more concise form: x3. This notation, known as exponentiation, indicates that 'x' is raised to the power of 3, or cubed. In mathematical terms, this signifies multiplying x by itself three times.
On the other side of the equation, we encounter the number 2, a constant. This number serves as a fixed point of reference within the mathematical equation, providing a specific target for the cubed value of 'x'. Our objective is to determine the precise value of 'x' that makes the equation x xx = 2 a true statement, where the cubed value of 'x' equals 2.
To comprehend the equation "x xx is equal to 2," we must start with the fundamental building blocks of algebra. Let's break down this equation step by step to grasp its essence.
- Pepper0 Comics Family Anime Manga Art Styles Explore Now
- Desi Mms Videos Hot Indian Girls Couples Watch Now
Let's proceed step by step:
Start by isolating x on one side of the equation.
Take the cube root of both sides to cancel out the exponent.
Simplify the left side of the equation.
Hence, the solution to the x xx is equal to 2 [ x3 = 2 ] to find \( x \), take the cube root of both sides:
\[ x = \sqrt[3]{2} ] approximating the value:
\[ x \approx 1.2599 ] if you need the exact cube roots in complex form, they are:
\[ x = \sqrt[3]{2}, \quad x = \sqrt[3]{2} \cdot e^{2\pi i \/ 3}, \quad x = \sqrt[3]{2} \cdot e^{4\pi i \/ 3} ] which simplifies to:
The expression x xx is equal to x3, which represents x raised to the power of 3. In mathematical notation, x3 means multiplying x by itself three times.
The solve for x calculator allows you to enter your problem and solve the equation to see the result. Solve in one variable or many. Understanding the basics x xx is equal to 2.
In mathematical exploration, we encounter various symbols and notations, each carrying its unique significance. The variable 'x', in particular, stands as a versatile symbol, a placeholder for an unknown quantity. These symbols represent unknown quantities, waiting to be unveiled. In the case of "x xx is equal to 2," 'x' serves as the elusive entity that we aim to discover.
The expression 'xxx' within the equation signifies a mathematical operation called "cubing." This operation involves multiplying 'x' by itself three times. Consider this example, the equation x xx is equal to 2, or equivalently, x3 = 2, represents a mathematical problem. To solve for x, we're essentially trying to find the number that, when cubed, equals 2. The solution involves finding the cube root of 2. The cube root of 2 is approximately 1.2599.
The exploration of mathematical equations extends beyond the mere numerical value. It involves the application of logical reasoning, algebraic manipulation, and the understanding of fundamental mathematical principles. By breaking down complex equations into their constituent parts, we gain insight into the underlying mathematical relationships and unlock the secrets held within the symbols.
Let's briefly consider the context of mathematical problem-solving. Many resources are available to aid in solving such equations. Calculators dedicated to solving equations for 'x' are readily accessible, allowing users to input the problem and automatically receive the solution. These tools often offer the ability to solve equations involving one or more variables, providing a valuable resource for both students and professionals alike.
Mathematics, at its essence, is a language. It provides a means to express and comprehend relationships between numbers and quantities. The equation "x xx is equal to 2" serves as a simple yet profound example of this language in action. Through careful analysis and step-by-step problem-solving, we can demystify this seemingly simple equation and discover the value of the unknown variable, 'x'.
Now, let's shift our focus to another aspect. The equation "x xx is equal to 2" might seem a solitary example, but it belongs to a broad category of equations. Equations are essentially statements of equality, asserting that two expressions hold equivalent values. In this case, we are stating that the cube of 'x' is equal to 2. This establishes a relationship between an unknown and a known quantity, opening the door to further analysis.
Mathematics is not just about finding numerical values; it also requires an understanding of concepts and principles. The act of solving an equation such as x3 = 2, requires knowledge of exponentiation, cube roots, and the order of operations. Without a firm grasp of these fundamentals, it would be difficult, if not impossible, to arrive at a correct solution.
We can consider the equation x3 = 2 in the context of real-world applications. While it may seem abstract, such equations can be used to model many phenomena. Whether it's calculating the volume of a cube or analyzing growth patterns, mathematical equations can act as powerful tools. The constant 2 in our equation can represent a specific quantity, and by finding the value of x, we gain further insights into the underlying context.
The versatility of mathematical equations is a testament to their enduring influence. They are not limited to a single field or domain. From physics to economics, from engineering to computer science, mathematical equations provide the framework for constructing models, solving problems, and making accurate predictions. The equation x3 = 2 is a humble yet effective illustration of this versatility.
The expression x xx can be represented as x3, which means multiplying x by itself three times. The expression x3 is a function, and the act of "cubing" a number is a mathematical operation in itself. The process of taking a number and multiplying it by itself a specific number of times (in this case, three) is a core concept in mathematics.
The equation "x xx is equal to 2" serves as a basic example that can be extended to encompass more complex equations. By understanding the processes involved in solving this simple equation, we set the stage for more involved applications. Learning to identify, analyze, and solve a straightforward equation helps develop the logical reasoning skills that can be applied across the field of mathematics.
If we wanted to approach this from a purely technical perspective, we'd want to isolate 'x' from the rest of the equation. This is done by taking the cube root of both sides of the equation. Taking the cube root "undoes" the cubing operation, so the equation becomes x = cube root of 2. This is the essential process of solving for 'x'.
The cube root of 2 is an irrational number, meaning that it cannot be expressed as a simple fraction. However, we can express this in the format of x 1.2599. Alternatively, the exact cube roots in complex form are:
\( x = \sqrt[3]{2}, \quad x = \sqrt[3]{2} \cdot e^{2\pi i \/ 3}, \quad x = \sqrt[3]{2} \cdot e^{4\pi i \/ 3} \)
The key takeaway is this: to solve an equation like x3 = 2, the fundamental method involves isolating the variable by performing the inverse mathematical operation.
Let us move away from mathematics briefly. Another topic is the American spy fiction action film series "xXx" (stylized as xxx and pronounced triple x), created by Rich Wilkes. The series consists of the films "xXx" (2002), "xXx: State of the Union" (2005), "xXx: Return of Xander Cage" (2017), and a short film: "The Death of Xander Cage".
Also there are various other apps such as Doubtnut. Doubtnut is no.1 study app and learning app with instant video solutions for ncert class 6, class 7, class 8, class 9, class 10, class 11 and class 12, iit jee prep, neet preparation and cbse, up board, bihar board, rajasthan board, mp board, telangana board etc.
To get the answer to your question :writing_hand:the equationd xxx 2 is satisfied when x is equal to.
- Hdhub4u Risks Of Free Streaming Legal Alternatives Explained
- Unveiling The Brighton Butler Divorce Details Insights
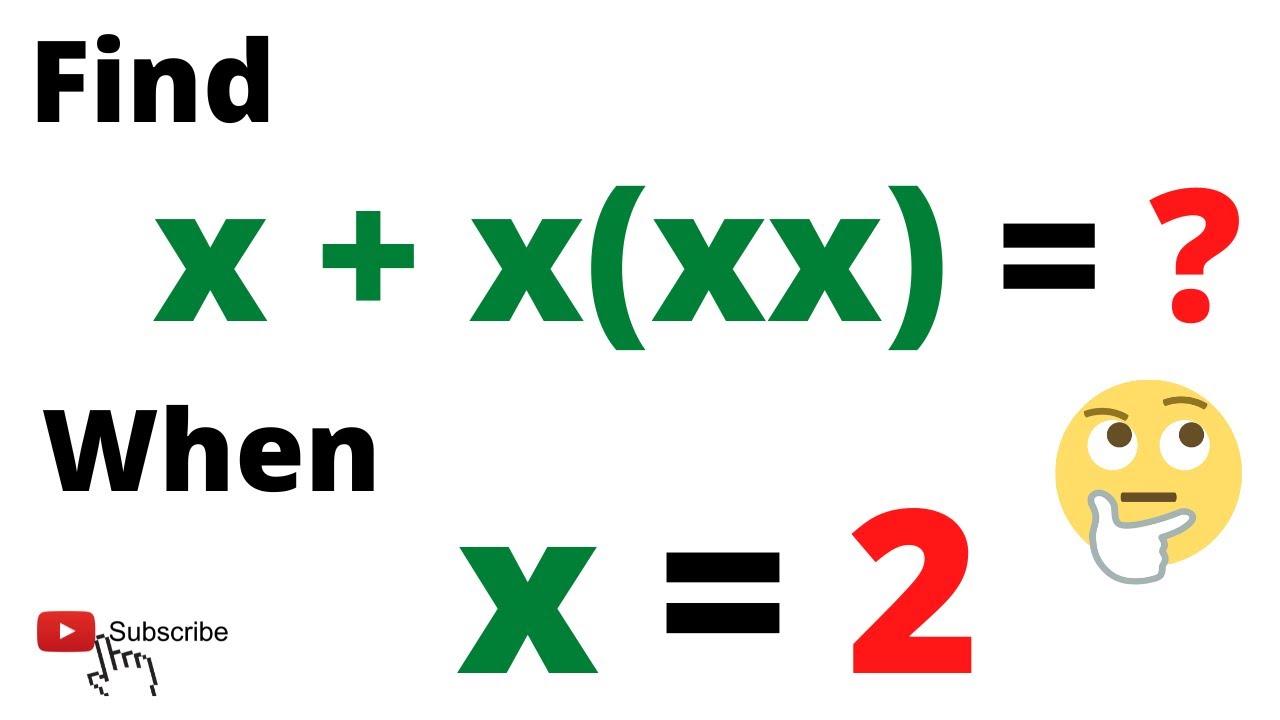
The value of x + x(xx) when x = 2 is Find the Answer in Seconds

Ex 12.3, 6 Simplify expressions and find value if x is equal to 2

Solve Linear Inequality with Parentheses 2x 3(x+4) is Greater Than or